Curve sketching

You da real mvps. Find critical numbers numbers that make the first derivative 0 or undefined.

Pin On Calculus

Sketch asymptotes and x and y intercepts where applicable.

. Thanks to all of you who support me on Patreon. Absolute x or x. So this is consistent.

Thus since the derivative increases as x increases f is. Curve sketching is a calculation to find all the characteristic points of a function eg. The above examples also contain.

Curve sketching Use Key. Next find the y-intercept substitute x 0 into the. Curve Sketching 57 Curve Sketching In this section we discuss how we can tell what the graph of a function looks like by performing simple tests on its derivatives.

Follow these steps for sketching a curve. The graph will cross the x-axis when y 0 and the y-axis when x 0. Curve sketching the process of predicting the functions graph given its expression.

Curve Sketching Using Calc. If we have a graph. The modulus or absolute value.

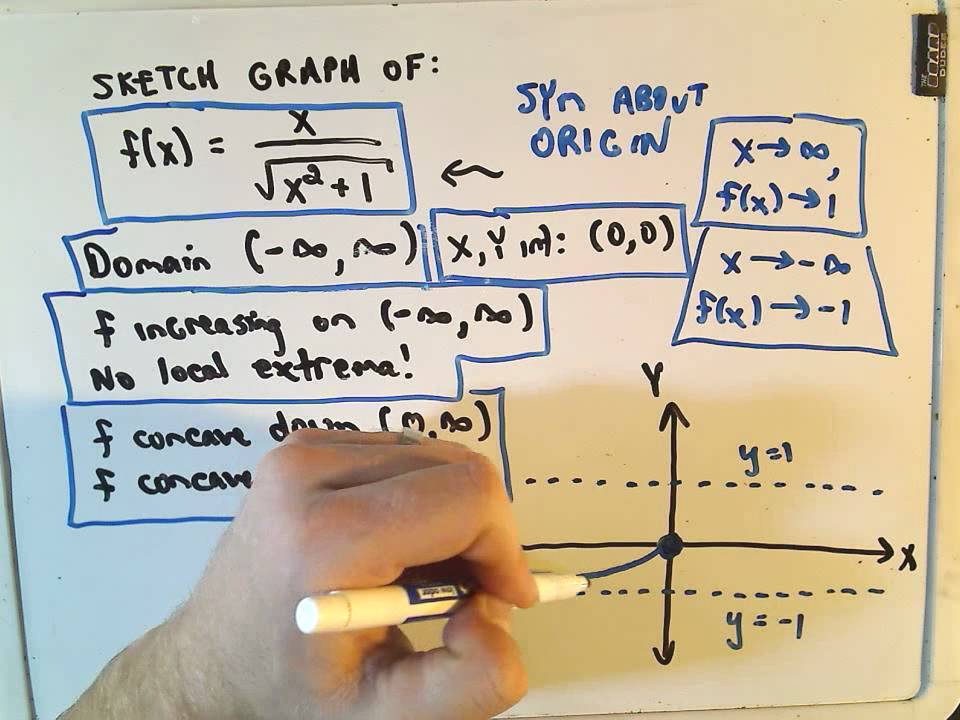
Techniques of Calculus 1 43 Curve Sketching Curve Sketching This section examines some of the interplay between the shape of the graph of f f and the behavior of f. Sketch the following curve by finding intercepts maxima and minima and points of inflection. A curve often gets very close to an asymptote without actually crossing it.

Lets put it all together. Figure 455a shows a function f with a graph that curves upward. Now lets see what happens when x is right less than when x is just barely.

Ad Read Customer Reviews Find Best Sellers. As x increases the slope of the tangent line increases. From 0 to 23 we are concave downwards and then at 23 we become concave upwards.

Displaystyle y x 3- 9 x y x3 9x Answer General Shapes If we learn the general. Even and odd functions. Connect these points with curves exhibiting the proper concavity.

Get step-by-step solutions to your Curve sketching problems with easy to understand explanations. The concepts of domain limits derivative extreme values monotonicity and concavity have been introduced. The oblique asymptote of the graph of a function.

It shows you how to graph polynomials rational functions with horizontal vertical asymptotes and. Square roots sqrt x cubic. In geometry curve sketching or curve tracing are techniques for producing a rough idea of overall shape of a plane curve given its equation without computing the large numbers of.

Curve sketching or curve tracing includes techniques that can be used to produce a rough idea of overall shape of a plane curve given its equation without computing the large numbers of. This calculus video tutorial provides a summary of the techniques of curve sketching. Solve Curve sketching problems with our Curve sketching calculator and problem solver.

Now it is time to combine these concepts together to plot. 571 The First Derivative. Firstly identify the general shape of the curve and whether it is of a negative or positive shape.

Roots y-axis-intercept maximum and minimum turning points inflection points. Knowing how to graph a. Free 2-Day Shipping wAmazon Prime.

Work out where the graph crosses the axes. It is also an application of our knowledge on first and second derivative tests. Here are some general curve sketching rules.

How to get those points. 1 per month helps.

Pin On Calculus